
#数楽 添付画像の試験問題は「良問」だったようだ。色々躓く要素が含まれている。問題のもとネタはスターリングの公式のある証明(そこそこ易しい)の一部分。pic.twitter.com/u9xO6khYyn
#数楽 まず、与えられた実数yに対してnを十分に大きくすればy>-√nになることに注意。y>-√nのときのf_n(y)の式の対数の極限を計算すればよい。対数をとったあとにTaylor展開すれば極限の計算は易しい。数学科の学生は各点収束より強い結果を示す練習をするとよい。

#数楽 グラフhttp://www.wolframalpha.com/input/?i=plot%20z=e^(-√(n)y)(1+y/√(n))**n for n=1,2,3,4,5 …たとえば、y<0でnについて単調増加、y>0では単調減少になっていそうなことがわかる。pic.twitter.com/NNeQ2rBH5s
#数楽 WolframAlphaのようなツールのおかげで解析学を非常に勉強し易くなっていると思う。ほんとおすすめ。なんとなく数式をふくむ英文っぽい入力にそれなりの答えを返してくれる。

#数楽 より精密な近似の様子を見るためにはplot z=e^(-√n y-y**3/(3√n))(1+y/√n)**n for n=1,2,3,4,5http://www.wolframalpha.com/input/?i=plot%20z=e^(-√n y-y**3/(3√n))(1+y/√n)**n for n=1,2,3,4,5 …pic.twitter.com/K565z17S7i
#数楽 近未来には既存のすべての数学がコンピューターネットワーク上にのっかるようになる(べきだ)と思う。もしもそのようなものが無料で誰でも使えるようになれば現在では想像できなかったような技術革新が生じると思う。
#数楽 コンピューターネットワーク上に実現された「数学」に一部の人しかアクセスできない未来は不愉快なので、そうならないことを祈りたい。特に子供が自由にアクセスできないようになるのはよろしくないと思う。

#数楽 添付画像はn=30の場合。青線がq=1/3の二項分布の確率の対数の-1/n倍のグラフ。赤線が対応するKullback-Leibler情報量のグラフ。n→∞でこれらは一致する。pic.twitter.com/9TyZbWScZj

#数楽 それら(KL情報量とその最小値でのTaylor展開の二次部分)のグラフの比較。p=1/3の近傍での近似の良さが本質的に二項分布の中心極限定理を意味しています。全体でもそこそこよい近似になっている。pic.twitter.com/2VPLkJWrUg
#数楽 上の方のグラフをWolframAlphaで得るためのURLshttp://www.wolframalpha.com/input/?i=plot%20y=-(1/30)log(binomial(30,30p)(1/3)**(30p)(2/3)**(30-30p)) and y=p log(p/(1/3))+(1-p)log((1-p)/(2/3)) for 0
#数楽 Re:self-RTsStirlingの公式n!〜n^n e^{-n}√(2πn)Hardy-Ramanujanの定理p(n)~exp(π√(2n/3))/(4√3 n)ここでp(b)は分割数これらの公式では定数因子まで正確に求まっている。
#数楽 Stirlingの公式の素朴な見方の1つ→「1からnまでの数を重複を許してランダムにn個選ぶとき、n個の数字が互いに異なる確率は√(2πn)/e^nで近似される」1/e^nだけで挙動をかなりわかった気になれるが、より精密に√(2πn)までわかっている点がうれしい。
#数楽 「1からnまでの数を重複を許してランダムにn個選ぶとき、n個の数字が互いに異なる確率」という稀なことが起こる確率はおおよそnの指数函数分の1の速さで小さくなることが、√(2πn)/e^nの中の1/e^nの部分からわかります。√nの影響は相対的に小さい。
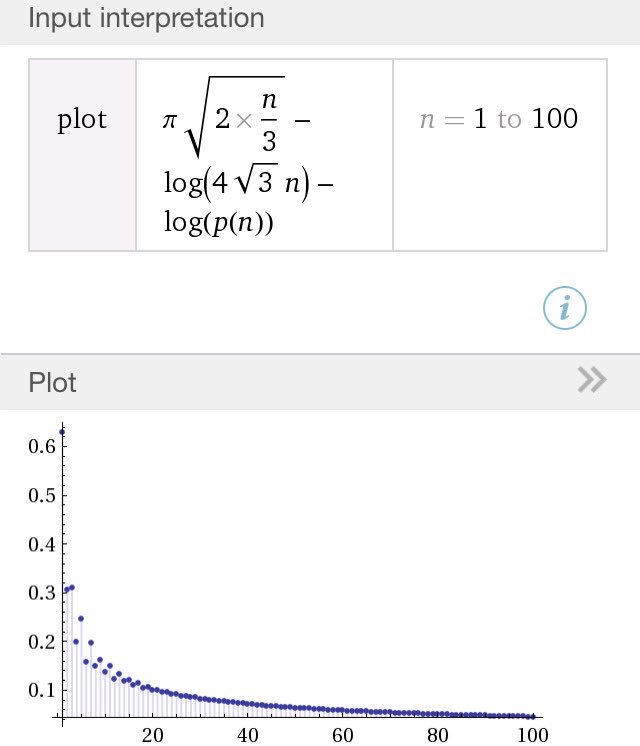
#数楽 Hardy-Rananujanの定理の数値的確認。[exp(π√(2n/3))/(4√3 n)]/p(n) の対数をプロット。n→∞で0に収束。http://www.wolframalpha.com/input/?i=plot%20y=π√(2n/3)-log(4√3 n)-log(PartitionP(n)), 1
#数楽 Hardy-Ramanujanの定理から、分割数p(n)の対数はおおよそnの平方根オーダーで増加することがわかるが、log(4√3 n)の項までわかっているのがうれしい。(Stirlingの公式の場合と同様にもっと精密な結果が得られている。)

#数楽 添付画像中の[In]は http://www.jstor.org/stable/1970462 です。 pic.twitter.com/oFz5dRpRMgモジュラー変換性から係数の漸近挙動を得るTauber型定理!
#数楽 http://projecteuclid.org/download/pdf_1/euclid.mmj/1028998729 …これはNewmanさんによる分割数に関するHardy-Rananujanの定理のsimplified proof. 最後は分割数p(n)を近似する数列q(n)の定積分表示にLaplaceの方法を適用する。
#数楽 たぶんNewmanさんの方針でInghamさん[In]のモジュラー変換性から係数の漸近挙動を出すTauber型定理も証明できると思うので、誰かそういう解説文を書いてくれないかなあ(もしくは見つけて来てくれないかなあ)と思っています。
#数楽 x=t^2, y=t^3は「x=f(t), y=g(t)の軌跡を考える。f(t)もg(t)も滑らかな函数なのに軌跡は滑らかではない例を挙げよ」の例になっています。 http://www.wolframalpha.com/input/?i=x=t**2, y=t**3 …y^2=x^3は退化した楕円曲線の例にもなっている。
#数楽 http://www.wolframalpha.com/input/?i=parametric plot x=t**2, y=t**3, z=t …parametric plot x=t**2, y=t**3, z=txyz空間内の曲線としてこれは滑らかだが、xy平面に射影すると尖がる。

#数楽 P(χ^2(d)>d log n), d=1, n=100の計算→3.2%http://www.wolframalpha.com/input/?i=P(X%3Elog+100),+chi+square+distribution+for+ν=1 …
#数楽 続き。指数型分布族は統計力学におけるカノニカル分布とほぼ同じ概念。指数型分布族は等確率の原理を仮定しない場合のカノニカル分布。その辺の話も例のノートで簡単に解説しておいた→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … の第2節
#数楽 ガンマ分布をいじっているとディガンマ函数ψ(s)=d(log Γ(s))/dsが出て来る。手計算で近似計算したい場合にはψ(s)=log s-1/(2s)+O(1/s^2) (s→∞)という近似を使うとよいと思う。 http://www.wolframalpha.com/input/?i=plot+y=ψ(s)-log+s+1/(2s),+0
#数楽http://togetter.com/li/1042730 このツイートが繋がっている返答連鎖のまとめ。画像はベイズ統計と関係ない。小島寛之氏のベイズ本をおすすめしているが、個人的には小島氏のベイズ本を他人にすすめるのは避けた方がよいと思う。
#数楽 再掲 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-05-01 … → http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … 例のノートVer.0.15(57頁)。簡単なTauber型定理とそのWallisの公式とx-x^2+x^4-x^8+x^{16}-…のx→1での様子への応用を追加。
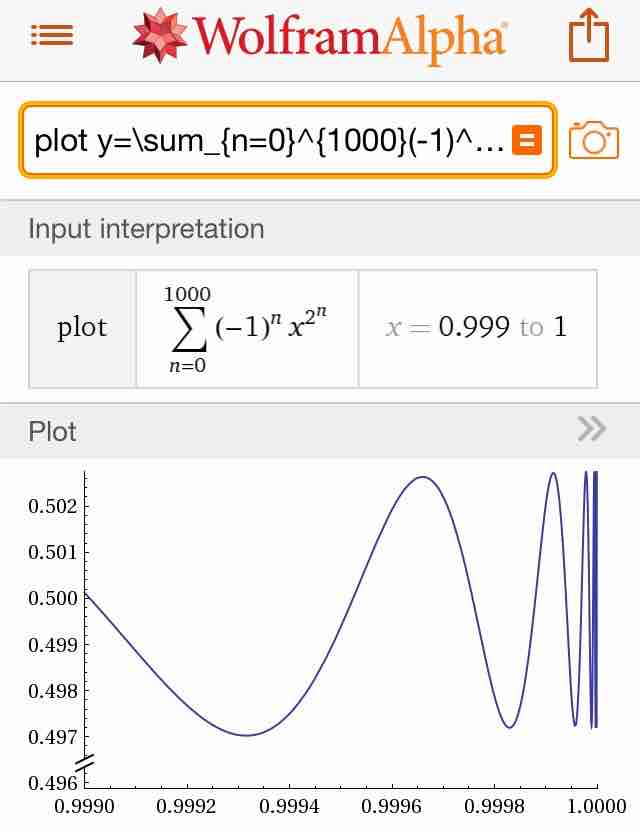
#数楽 WolframAlphaで x-x^2+x^4-x^8+x^{16}-…の0.999<x<1のでのグラフを書いてみた。確かに無限に振動しているっぽいよね(実際している)。pic.twitter.com/ESzdYarf17
#数楽 再掲 https://www.uam.es/personal_pdi/ciencias/dragan/respub/Duren_Tauberian_Talk_2013-10_UAM.pdf … ←これに x-x^2+x^4-x^8+x^{16}-…のx↑1での漸近挙動に関する詳しい解説があります。収束しないことはTauber型定理からすぐにわかる。
https://twitter.com/ysmemoirs/status/799003733468135424 …#数楽 ううむ、暗記で処理されちゃうかあ…・点と直線の距離・三角関数の加法定理・微分の定義・1/6公式微分の定義が「暗記で行ける」を促すというのだけはわからないが、残りの3つも暗記で処理するとつまらない。続く
#数楽 点(p,q)と直線ax+by+c=0の距離dはd=|ap+bq+c|/√(a^2+b^2)となるという結果の絶対値を外した版は一次函数z=ax+by+cのグラフがベクトル(a,b)の方向に傾き√(a^2+b^2)の登り坂の傾いた平面になることを意味しています。続く
#数楽 続き。点と直線の距離の公式は、一次函数z=ax+by+cの値の絶対値は直線z=0と点(x,y)の距離に比例し、比例定数は√(a^2+b^2)になることを意味します。そしてベクトル(a,b)は直線z=0に垂直。これで函数z=|ax+by+c|の形がわかるわけです。続く
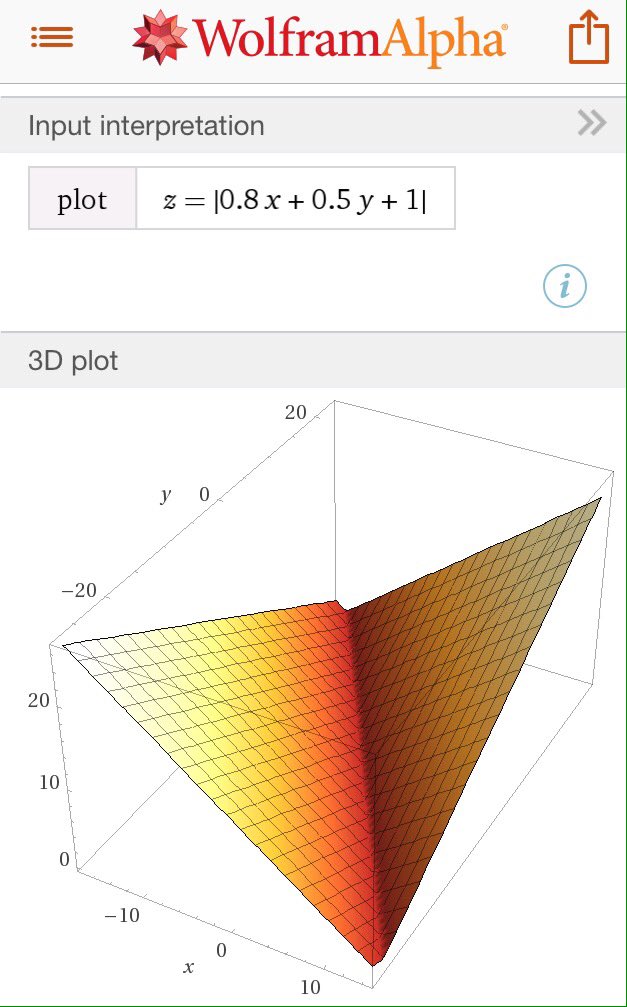
#数楽 z=|ax+by+c|のグラフの形は谷型になります(添付画像)。WolframAlphaの有料アプリにはお金を払う価値があります。適当に数学的情報を入力すると関連の情報を返してくれる。裏でMathematicaが動いています。入力が適当で良い所がいい!続くpic.twitter.com/NKiUipiwkI

#数楽 点と直線の距離の公式は、ax+bの絶対値はxと-b/aの距離に比例し、比例定数が|a|になることの一般化になっています。y=|ax+b|のグラフも谷型になる。続くpic.twitter.com/p9giQyi4AE
#数楽 続き。しかし、普通は絶対値を取る前のy=ax+bのグラフについて先にやるのが普通です。それは傾きがaの傾いた直線の形になる。点と直線の距離についても、z=ax+by+cのグラフの傾き方がベクトル(a,b)で表されるという理解の方が基本的です。続く
#数楽 z=ax+by+cのグラフの傾き方を知っていることはものすごく重要です。y=ax+bのグラフの傾き方を知らないと困るこたと同じ。2変数函数の微分の概念は2変数函数を局所的にz=ax+by+cの形の函数で近似することによって得られます。続く
#数楽 続き。z=ax+by+cのグラフの形を知らないと、2変数函数の微分が何をやっているのか理解不能になります。しかし、そのグラフの傾き方を知っていると、接平面の傾き方が偏微分で与えられることがものすごくよくわかる。この直観は数学の実用的な応用のためには必須だと思う。続く
#数楽 続き。所謂Cauchy-Schwarzの不等式の話も以上の話の範疇に含まれます。そういう話は以前次のリンク先に書きました。https://twitter.com/genkuroki/status/793223250444554240 …
#数楽 せっかく受験勉強するならば、くだらない受験のためではなく、実際に数学を応用することを見据えて普遍的に役に立つ見方を学んだ方がよいと思う。そして、大学で数学を教えている人達はそういう勉強に誘導できる入試問題を出せたらよいと考える傾向が強いと思う。続く
#数楽 続き。1/6公式なんぞをやる余裕があるなら、ベータ函数まで一般化してしまった方がすっきりします。ベータ函数は応用上知っていないと困る知識の1つなので受験勉強のついでに触れるのはとてもよいことだと思います。詳しくは→https://twitter.com/genkuroki/status/735246658334691328 …
#数楽 続き。「点と直線の距離の公式」とか「1/6公式」とかの暗記とか言うと全くくだらない話になってしまうのですが、函数z=ax+bx+cのグラフの様子とかベータ函数とかの話にすればそれは知っておいた方がよい普遍的な知識になります。ほんの少し溝を飛び越えるだけだ面白い話になる。
#数楽 学生と話をすると、結構、いい先生にあたったおかげで数学が好きになった学生が多いような印象を受けます。大学で数学を教えていると高校や予備校の数学の先生には感謝することが多いです。でもほんの一部の学生に受験数学のくだらない面の被害を見付けて悲しくなることがある。
#数楽 続き。効率的に本格的な考え方と健全な直観を育てて行かなければ実際の応用で使われるレベルの数学の理解に達することは無理です。個人的な意見では、受験勉強の段階からそういうことを意識できる人の方が受験でも有利になると思う。若い人達にとってモチベーションの違いは大きいと思う。
#数楽 単に大学受験をクリアするために勉強するのと、最先端の科学や技術を理解することを見据えて勉強するのでは、どちらの方が興奮できるか?私個人は絶対に後者だと思う。所謂文系学部学科でも統計学を知らないと色々不利になります。数学は強力な矛にも盾にもなります。
#数楽 続き。所謂文系諸学問で重要なのは権威的な議論に対する健全な批判精神。数学的な道具を権威的に使うことに対抗するには数学的に無知であってはまずい。少なくとも助けてくれる数学に強い人と話せるだけの教養は必要。自分にできないことは他人に頼ればよいのですが、頼るにも知識が必要です。
#数楽 続き。たとえば、統計処理をした結果のp値を報告している人が何か怪しいことを言っているように感じたとします。そのときに「そのp値はどのような前提における何の確率なのかを教えて下さい」と質問できるだけの教養と度胸があると怪しい言説を粉砕できる可能性が飛躍的に高まると思う。
#数楽 続く。もしもクリアな回答が返って来ずに、p値の定義さえ知らずに統計処理をやっていることがわかったなら、そこを徹底的に攻めて潰しにかかるのが世のため人のためになる行為だと思います。統計学用語は権威的に響くようにカスタマイズされていることが多いのですが、理解すれば怖くない。
#数楽 あと、今の高校生の大部分はiPhoneまたはAndroid携帯を持っていると思う。WolframAlphaの有料アプリを保護者に購入してもらうべきだ。ただしカンニングには絶対に使用しないこと!かなり強力に数学の問題の答えを教えてくれる。グラフ作画はとても便利。続く
#数楽 リンクメモhttps://www.google.co.jp/search?q=WolframAlpha+使い方 …WolframAlphaの使い方の検索http://twilog.org/genkuroki/search?word=WolframAlpha&ao=a …私によるWolframAlphaの使用例
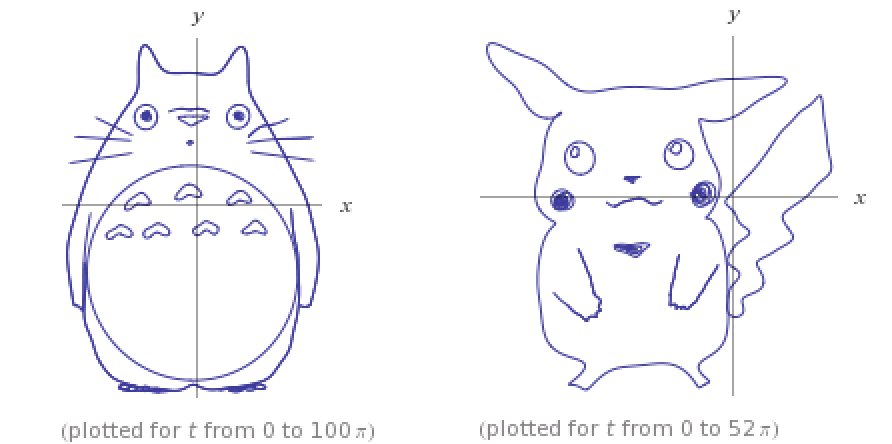
#数楽 https://twitter.com/asuka_tsukimi/status/811831661516029952 …答えを知りたいだけならばWolframAlphaがとても便利。私はWAを使わない日がない。スマホユーザーはWAの有料アプリを入れておく価値があると思う。ウェブブラウザで無料で使うとCPUの制限が厳しい。続く
#数楽 http://www.wolframalpha.com/input/?i={%7B1,1,6},{-1,3,6},{1,-1,-1}} …WolframAlphaに行列を入力するだけだJordan標準形も教えてくれる。
#数楽 続き。サイズの小さな行列のジョルダン標準形は固有値が求まるケースでは容易に計算できる。3×3行列Aの固有値α,β,γが求まったとする。(1)固有値が3つとも互いに異なれば対角化可能。続く
#数楽(2)α≠β=γのときジョルダン標準形の可能性は2通りしかない。(A-αE)(A-βE)=0ならば対角化可能になり、そうでないならばβの方が2×2のジョルダンブロックになる。続く
#数楽(3)固有値が全部等しいとき、ジョルダン標準形は3通りのどれかになる。A-αE=0ならば対角化可能であり、そうでなくて(A-αE)^2=0ならば2×2のジョルダンブロックが出て来て、どちらでもないなら3×3のジョルダンブロックがジョルダン標準形になる。
#数楽 さらに少し工夫すれば行列を適当にかけて列ベクトルを適切に選んで並べれば、連立一次方程式を一度も解かずに、もとの行列を相似変換でジョルダン標準形にしてくれる可逆な行列を求めることもできる。
#数楽 3×3行列のジョルダン標準形にはサイズが2以上のジョルダンブロックが2つ以上出て来ることがないので、様々な計算を手抜きできる。4×4行列以上のジョルダン標準形をいじらないとジョルダン標準形に関する典型的な状況を扱ったことにはならない。
#数楽 4×4行列Aの固有値がαだけのとき、A-αE≠0かつ(A-αE)^2=0ならば、Aのジョルダン標準形の可能性は2×2のジョルダンブロックが1つの場合と2つの場合の2通り。そしてA-αEのランクと2×2のジョルダンブロックの個数は等しい。ランクの計算は基本的。
Re:RT #数楽√(2π)はほぼ2.5なんだよね。e/(1+1/12)=12e/13もほぼ2.5なので、√(2π)/e×(1+1/12)はほぼ1になる。これは偶然ではなくて第1補正項付きのスターリングの公式のn=1の場合。http://www.wolframalpha.com/input/?i=�%88�(2π)/e×13/12 …



